Статистические критерии риска

Кроме того, описанные выше критерии предполагалось применять к нормальному распределению вероятностей. Оно, действительно, широко используется при анализе рисков финансовых операций, т.к. его важнейшие свойства (симметричность распределения относительно средней, ничтожная вероятность больших отклонений случайной величины от центра ее распределения, правило трех сигм) позволяет существенно упростить анализ. Однако не все финансовые операции предполагают нормальное распределение доходов (вопросы выбора распределения рассмотрены более подробно чуть ниже) Например, распределения вероятностей получения доходов от операций с производными финансовыми инструментами (опционами и фьючерсами) часто характеризуется асимметрией (скосом) относительно математического ожидания случайной величины (рис. 1).

Так, например, опцион на покупку ценной бумаги позволяет его владельцу получить прибыль в случае положительной доходности и в то же время избежать убытков в случае отрицательной, т.е. по сути, опцион отсекает распределение доходности в точке, где начинаются потери.

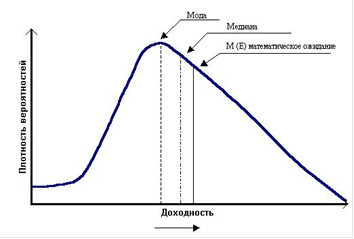
Рис.1 График плотности распределения вероятности с правой (положительной) асимметрией

В подобных случаях использование в процессе анализа только двух параметров (средней и стандартного отклонения) может приводить к неверным выводам. Стандартное отклонение неадекватно характеризует риск при смещенных распределениях, т.к. игнорируется, что большая часть изменчивости приходится на «хорошую» (правую) или «плохую» (левую) сторону ожидаемой доходности. Поэтому при анализе асимметричных распределений используют дополнительный параметр - коэффициент асимметрии (скоса). Он представляет собой нормированную величину третьего центрального момента и определяется по формуле:

риск инвестиционный актив портфель

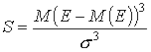
Экономический смысл коэффициента асимметрии в данном контексте заключается в следующем. Если коэффициент имеет положительное значение (положительный скос), то самые высокие доходы (правый «хвост») считаются более вероятными, чем низкие и наоборот.

Коэффициент асимметрии может также использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равно 0.

В ряде случаев смещенное вправо распределение можно свети к нормальному прибавлением 1 к ожидаемой величине доходности и последующим вычислением натурального логарифма полученного значения. Такое распределение называют логнормальным. Оно используется в финансовом анализе наряду с нормальным.

Некоторые симметричные распределения могут характеризоваться четвертым нормированным центральным моментом - эксцессом (е):

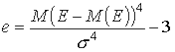
Если значение эксцесса больше 0, кривая распределения более остроконечна, чем нормальная кривая и наоборот.

Экономический смысл эксцесса заключается в следующем. Если две операции имеют симметричные распределения доходов и одинаковые средние, менее рискованной считается инвестиция с большим эксцессом.

Для нормального распределения эксцесс равен 0.

Выбор распределения случайной величины

Нормальное распределение используют, когда невозможно точно определить вероятность того, что непрерывная случайная величина принимает какое-то конкретное значение. Нормальное распределение предполагает, что варианты прогнозируемого параметра тяготеют к среднему значению. Значения параметра существенно отличающиеся от среднего, т.е. находящиеся в “хвостах” распределения, имеют малую вероятность осуществления. Такова природа нормального распределения.

Треугольное распределение представляет собой суррогат нормального и предполагает линейно нарастающее по мере приближения к моде распределение.

Трапециевидное распределение предполагает наличие интервала значений с наибольшей вероятностью реализации (НВР) в пределах РВД.