Кривые безразличия

Инвестор стремиться создать эффективный портфель, который максимизирует доходность при заданном уровне риска, или уменьшить риска при заданном уровне доходности.

Из проведенных расчетов можно сделать вывод, что процедура диверсификации позволяет снизить риск портфеля по сравнению с риском отдельных активов. Таким образом, коэффициент корреляции должен быть как можно ближе к значению «-1», это будет свидетельствовать о том, что портфель будет более эффективным и, следовательно, нужно в дальнейшем анализировать проекты АВ и БВ.

Рассчитав ожидаемую доходность и уровень риска каждого из проектов, можно сделать вывод, что инвестору лучше всего вкладывать свои инвестиции в портфель АВ с ожидаемой доходностью 15,128% и уровнем риска 0,0525%, так как у этого портфеля доходность по сравнению с портфелем БВ выше и уровень риска ниже.

Портфель АВ содержит 45% актива А и 55% актива В.

Задача №3

Имеются следующие исходные данные

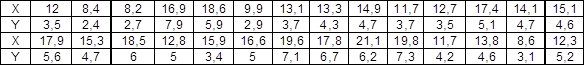
X - среднегодовая стоимость производственных фондов (млн.руб.)

Y - средне годовая выручка от продаж (млн.руб.)

По условиям задачи необходимо оценить зависимость между покупателями на основе проведения корреляционно-регрессионного анализа, который сводиться к измерению связи и установлению зависимости между x и y.

Необходимо построить, обработав статистическую информацию, регрессионную модель:

y = a + bx,

где: a и b - параметры уравнения регрессии, которые необходимо определить, проведя анализ.

Для нахождения a и b по методу наименьших квадратов, составляем расчетную таблицу.

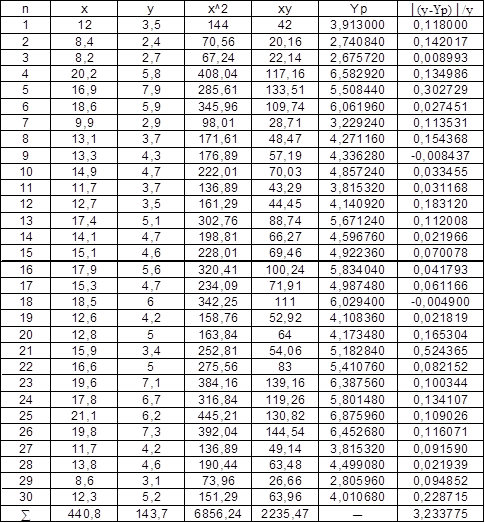
Полученные итоговые значения из расчетной таблице подставляем в систему нормальных уравнений:

{na + bx = ∑y

{a∑x + b∑x2 = ∑xy

{30a+440,8b=143,7 →

{440,8a+6856,24b=2235,47

{a=(143,7-440,8b)/30 →

{440,8*(143,7-440,8b)/30)+6856,24b =2235,47

,8 *(4,79-14,69b) + 6856,24b = 2235,47

2111,43-6475,35b+6856,24b=2235,47

,89b = 124,04

b = 0,3256

a = (143,7*440,8*0,3256)/30

a = 0,0058

Для проверки значимости полученной зависимости необходимо определить показатель среднего линейного отклонения - ε.

ε= 1/30*∑│y - Yp│/y * 100%

i=1

ε= 1/30*3,233775 * 100% = 10,78% < 15%

=> Уравнение можно использовать для прогнозных целей.

Подставляя в полученную зависимость планируемое значение показателя х, можно получить требуемый прогноз.

Задача №4

По полученному уравнению регрессии для среднегодовой величины годовой продукции на складе предприятия найти выручку от реализации на следующий год.

Составить бюджет движения денежных средств (БДДС) на следующий год и сделать раздвинутые выводы.

Исходные данные:

) Объемы продаж увеличиваются с темпом роста 1,5% в месяц;

) Компания проводит индивидуальную сбытовую политику при разных условиях оплаты:

25% - реализуется за наличный расчет,

75% - с отсрочкой от платежа на условиях 3/10 брутто 30, что означает предоставление отсрочки от платежа на 30 дней, а если товары оплачиваются в течении 10 дней, то предоставляется скидка 3%.

При этом 80% объемов продаж оплачиваются в следующем месяце. Из них: 25% со скидкой, а 20% оплачиваются еще с задержкой на один месяц.

) Сырье закупается в размере потребности следующего месяца. Расчеты с поставщиками производятся через месяц. Прогнозные изменения цен на сырье - 3% в месяц.

) Издержки определяются в % от выручки:

условно переменные (сырье) - 40%;

условно постоянные - заработная плата (15%), аренда производственных площадей (10%), прочие расходы (5%).

Уровень инфляции - 2% в месяц.

) Аренда и заработная плата выплачиваются в месяц, следующим за месяцем их возникновения.

) Единый социальный налог (ЕСН) - 26% от заработной платы.

Налог на прибыль - 20%.

) Планируется вкладывать средства в модернизацию производств (период и величина определяется самостоятельно).